昨天我們聊到 Polynomial Regression 是一種希望透過數據使用多項式預測函數來建模，並且未知的模型參數也是通過數據來估計的回歸模型。

今天我們來一起實做吧

Implementation

在這個部分，我們可以先使用 scikit-learn 的 library 來先試試看

如果尚未安裝，使用 pip install scikit-learn 來安裝 package

Prepare data

首先們先建立 3 團隨機產生數值的 cluster

# Number of data points in each cluster
num_points = 500

# Generate data for three clusters
cluster1 = np.random.normal(loc=[2, 2], scale=[0.5, 0.5], size=(num_points, 2))
cluster2 = np.random.normal(loc=[6, 6], scale=[0.7, 0.7], size=(num_points, 2))
cluster3 = np.random.normal(loc=[4, 8], scale=[0.4, 0.6], size=(num_points, 2))

# Combine the clusters
x = np.concatenate((cluster1[:, 0], cluster2[:, 0], cluster3[:, 0]))
y = np.concatenate((cluster1[:, 1], cluster2[:, 1], cluster3[:, 1]))

Create the polynomial features

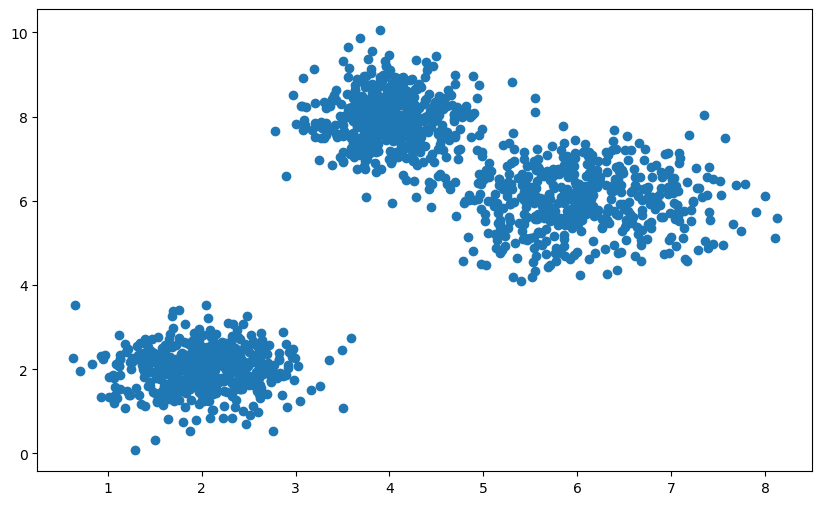
接著定義 polynomial features 的維度

degree = 1
poly = PolynomialFeatures(degree=degree, include_bias=True)
poly_features = poly.fit_transform(x.reshape(-1, 1)) # x.reshape(-1, 1) is a 2D array with one column

Create Model

透過建立 LinearRegression 來預測有哪一個參數可以來代表這些 cluster 的分佈

from sklearn.linear_model import LinearRegression

poly_reg_model = LinearRegression()
poly_reg_model.fit(poly_features, y)

y_predicted = poly_reg_model.predict(poly_features)

Evaluation

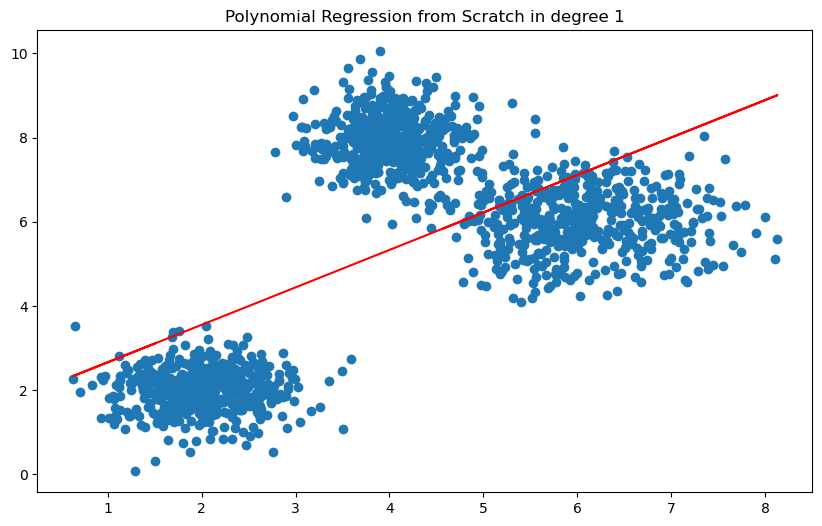
如昨天提及，我們可以透過 MSE 和 MAE 的 loss function 來判斷模型好壞

# calculate loss, MSE, MAE
from sklearn.metrics import mean_squared_error, mean_absolute_error

print("Accuracy: ", poly_reg_model.score(poly_features, y))
print("MSE: ", mean_squared_error(y, y_predicted))
print("MAE: ", mean_absolute_error(y, y_predicted))

Accuracy:  0.3770748813271505
MSE:  4.092465875195728
MAE:  1.791307625621191

From Scratch

在 From Scratch 的部分僅使用 numpy

Create the feature matrix

這裡 code 定義 CustomFeatureTransformer 用於進行特徵轉換

class CustomFeatureTransformer:
    def __init__(self, degree, is_bias=True):
        self.is_bias = is_bias
        self.degree = degree
    
    def transform(self, x = None):
        if x is None:
            raise ValueError('x is None')
        if self.is_bias:
            x = np.c_[np.ones(x.shape[0]), x]
        for i in range(2, self.degree + 1):
            x = np.c_[x, x[:, 1] ** i]
        return x
    
    def fit_transform(self, x):
        return self.transform(x)

__init__(self, degree, is_bias)

• degree（次數）：這是一個整數，表示要對特徵進行多少次方轉換。
• is_bias（偏差）：這是一個布林值，表示是否要添加偏差項（常數項）到特徵中。

transform(self, x)

這個用於對輸入的特徵進行轉換，它有一個參數x，表示輸入的特徵數據。這個方法執行以下步驟：

• 檢查x是否為None，如果是，則拋出ValueError異常
• 如果is_bias為True，則在特徵x的左側添加一列全為1的常數項，以添加偏差項
• 對特徵進行多項式轉換，將特徵的第二列（索引為1）提升到2次方、3次方，一直到degree指定的次數
• 返回轉換後的特徵x

Create Model

這裡 code 定義 CustomLinearRegression 的自定義線性回歸類別，用於執行簡單的線性回歸模型

class CustomLinearRegression:
    def __init__(self):
        self.w = None
    
    def fit(self, x, y):
        self.w = np.linalg.inv(x.T.dot(x)).dot(x.T).dot(y)
    
    def predict(self, x):
        return x.dot(self.w)
    
    def score(self, x, y):
        y_pred = self.predict(x)
        return 1 - ((y - y_pred)**2).sum() / ((y - y.mean())**2).sum()

fit(self, x, y)

這是訓練模型的方法
這裡使用兩個參數 x 和 y，分別代表輸入特徵和目標變數

• 計算 x 的轉置矩陣 x.T
• 計算 x 的轉置矩陣 x.T 與 x 的矩陣乘積 x.T.dot(x)
• 計算矩陣乘積的逆矩陣 np.linalg.inv(x.T.dot(x))
• 計算 (x.T.dot(x)).dot(x.T)，然後再與 y 相乘，得到最終的權重 self.w

predict(self, x)

這是用於進行預測的方法
這裡使用輸入特徵 x，並使用模型的權重 self.w 對輸入進行線性組合，返回預測值

Evaluation

class MAE:
    def __call__(self, y, y_pred):
        return np.mean(np.abs(y - y_pred))
    
    def gradient(self, y, y_pred):
        return np.sign(y - y_pred)
    
class MSE:
    def __call__(self, y, y_pred):
        return np.mean((y - y_pred)**2)
    
    def gradient(self, y, y_pred):
        return 2 * (y_pred - y)

在判斷 From scratch 是否實做成功，可以用 Evaluation 來觀察兩者輸出是否接近或相同

詳細 Notebook 可以參考 Github

明天要進入真實實戰部份，會透過 Kaggle competition 來演練